2012-01-10
11:03:31
Veckansmatteuppgift!
Här kommer årets första Matte uppgift för året 2012! :)
Uppgiften kommer inte att vara så svår att lösa utan ALLA kommer ha chans att lösa denna fantastiska uppgift.
Lycka till!
Uppgiften kommer inte att vara så svår att lösa utan ALLA kommer ha chans att lösa denna fantastiska uppgift.
Lycka till!
Bestäm konstanterna a och b så att:
f(x) = x3 +ax2 + bx
har ett lokalt maximum för x= -1 och ett lokalt minimum för x=3.
Bara att börja hugga in! :)
// Livetpaskid
Kommentarer:
#2:
Nilsson
Jag håller med om det svaret:)
Kommentera inlägget här:

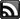

f(x)=x^3+ax^2+bx
f'(x)=3x^2+2ax+b
f'(-1)=f'(3)=0
-> 3(-1)^2+2a(-1)+b=0
-> 3(3)^2+2a(3)+b=0
-> 3-2a+b=27+6a+b
3-2a=27+6a
3-27=8a
-24=8a
a=-3
0=27-18+b
0=9+b
b=-9
SVAR: f(x)=x^3-3x^2-9x